This post talks about the construct of a quadratic equation and determines if a given equation is quadratic or not.
It has answers to the 1st question of NCERT X grade Exercise 4.1 problems on Quadratic Equations. Hope you find this useful.
Background
The standard form of a Quadratic Equation is
ax2 + bx + c = 0
Where a, b, c are all real numbers and the highest degree or power of the variable in the equation should be 2.
The operator can be + or -.
The 1st set of problems are given to evaluate if a given equation confirms to the quadratic equation requirements or not.
i) (x+1)2 = 2(x-3)
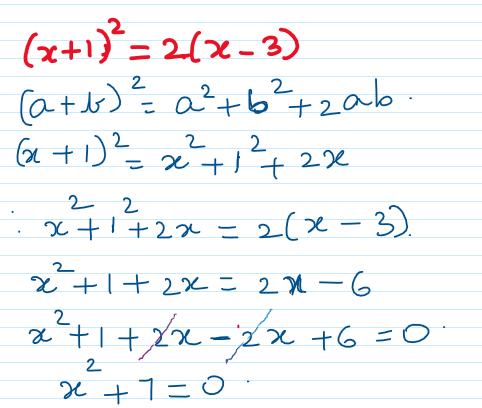
The highest degree of equation is 2.
x2 + 7 = 0 can be expressed as x2 + 0x + 7 = 0, which is same as the quadratic equation form
ax2 + bx + c = 0.
Hence (x+1)2 = 2(x-3) is a valid quadratic equation.
ii) x2 -2x = (-2)(3-x)
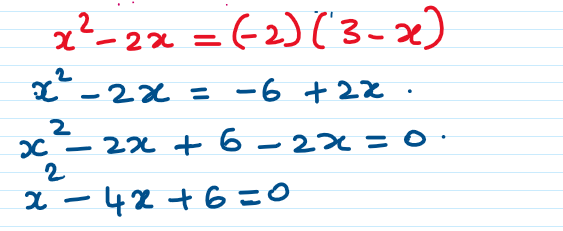
The highest degree of equation is 2 and x2 – 4x + 6 = 0, is also of the quadratic equation form
ax2 +bx + c = 0.
Hence x2 -2x = (-2)(3-x) is a valid quadratic equation
iii) (x-2) (x+1) = (x-1) (x+3)
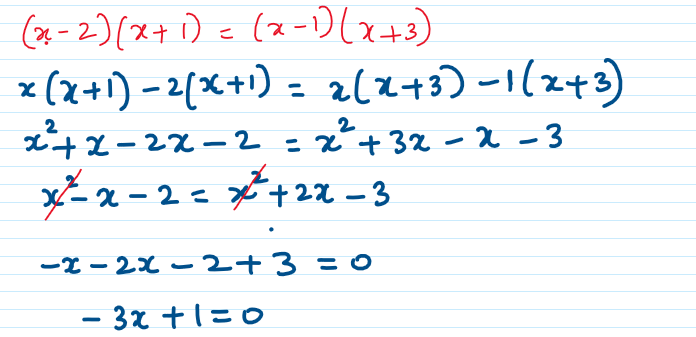
The highest degree of equation is 1.
-3x + 7 = 0 can be expressed as 0x2 – 3x + 7 = 0, which is same as the quadratic equation form
ax2 + bx + c = 0.
Hence (x-2) (x+1) = (x-1) (x+3) is a valid quadratic equation.
iv) (x -3) (2x + 1) = (x – 1)
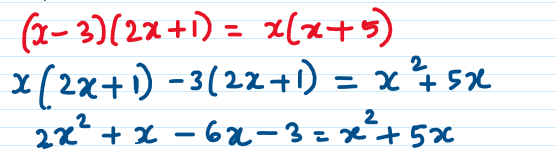
Combining like terms together
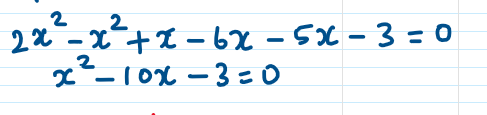
The highest degree of equation is 2.
x2 – 10x – 3 = 0 is having the quadratic equation form ax2 + bx + c = 0.
Hence (x -3) (2x + 1) = (x – 1) is a valid quadratic equation.
v) (2x – 1) (x-3) = (x + 5) (x – 1)
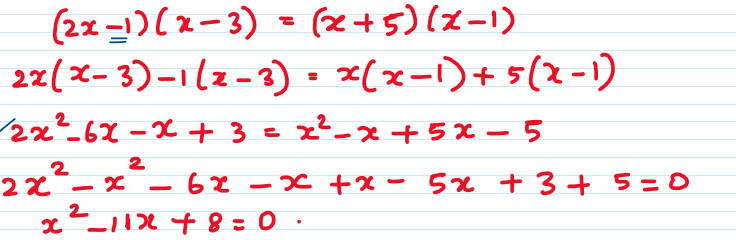
The highest degree of equation is 2.
x2 – 11x + 8 = 0 is having the quadratic equation form ax2 + bx + c = 0.
Hence (2x – 1) (x-3) = (x + 5) (x – 1) is a valid quadratic equation.
vi) x2 + 3x + 1 = (x – 2)2
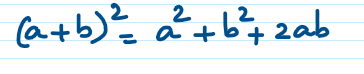
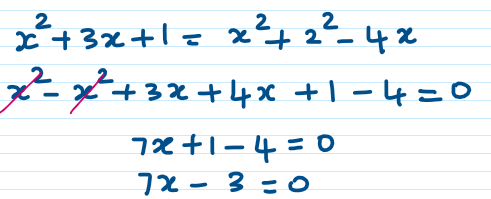
The highest degree of equation is 1.
7x – 3 = 0 can be expressed as 0x2 + 7x – 3 = 0, which is same as the quadratic equation form
ax2 + bx + c = 0.
Hence x2 + 3x + 1 = (x – 2)2 is a valid quadratic equation.
vii) (x + 2)3 = 2x(x2 – 1)
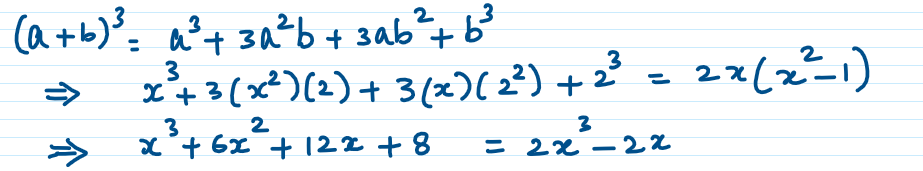
Combining like terms together
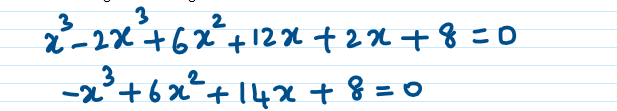
The highest degree of the equation is 3 and not 2. Hence the given equation (x + 2)3 = 2x(x2 – 1) is not a quadratic equation
viii) x3 – 4x2 – x + 1 = (x – 2)3
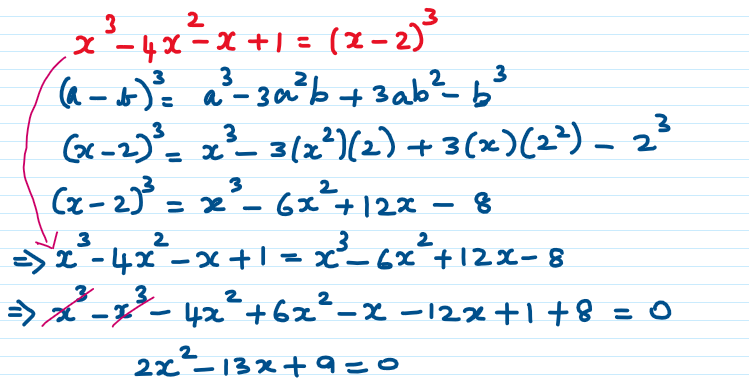
The highest degree of equation is 2.
x3 – 4x2 – x + 1 = (x – 2)3 results in a quadratic equation form ax2 + bx + c = 0.
Hence x3 – 4x2 – x + 1 = (x – 2)3 is a valid quadratic equation.